“12 công thức đạo hàm thường gặp trong đề thi 2021” giúp bạn có cái nhìn tổng quan về các đạo hàm thường gặp. Thông thường, bảng đạo hàm của hàm số sơ cấp cơ bản sẽ bao gồm hàm số đa thức, phân thức hữu tỉ, hàm số căn bậc hai, lũy thừa, mũ, lôgarit, đạo hàm hàm số lượng giác,…; và các quy tắc tính đạo hàm (đạo hàm của tổng, hiệu, tích, thương; đạo hàm hàm hợp). Cùng Top Uni ôn bài đạo hàm và chuẩn bị thật tốt cho bài kiểm tra nhé !

Khái niệm công thức đạo hàm tại một điểm

• Cho hàm số y=f(x) xác định trên (a;b) và x0∈(a;b):
  f′(x0)=limx→x0f(x)–f(x0)x–x0=limΔx→0ΔyΔx (Δx=x–x0,Δy=f(x0+Δx)–f(x0)
• Nếu hàm số y=f(x) có đạo hàm tại x0 thì nó liên tục tại điểm đấy.

Công thức đạo hàm căn bản

Định lý 1: Hàm số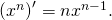 

Nhận xét:

(c)’=0 (với c là hằng số).
(x)’=1.
Định lý 2: Hàm số 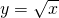 có đạo hàm với mọi x dương và: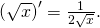 

Bí quyết đạo hàm tổng, hiệu, tích, thương

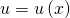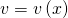Định lý 3: Giả sử  và  là các hàm số có đạo hàm tại điểm x thuộc khoảng nắm rõ ràng. Ta có:

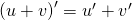
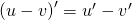
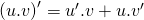
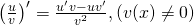    Mở rộng:

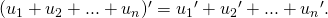 Hệ quả 1: Nếu như k là một hằng số thì: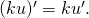 

Hệ quả 2: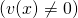 

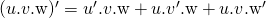
Bí quyết đạo hàm hàm hợp

Định lý: Cho hàm số 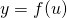 với 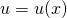 thì ta có: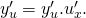 

Hệ quả:

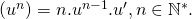
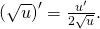
Master đạo hàm lượng giác

Công thức đạo hàm của hàm số y=sinx

Hàm số y=sinx có đạo hàm tại mọi x∈R và (sinx)′=cosx.

Nếu y=sin u và u=u(x) thì (sinu)′=u′.cosu.

Công thức đạo hàm của hàm số y=cosx

Hàm số y=cosx có đạo hàm tại mọi x∈R và (cosx)′=−sinx.

Nếu y=cos u và u=u(x) thì (cosu)′=−u′.sinu.

Công thức đạo hàm của hàm số y=tanx

Hàm số y=tan x có đạo hàm tại mọi x≠π2+kπ,k∈R và (tanx)′=1cos2x.

Nếu y=tan u và u=u(x) thì (tanu)′=u′cos2u.

Công thức đạo hàm của hàm số y=cotx

Hàm số y=cotx có đạo hàm tại mọi x≠kπ,k∈R và (cotx)′=–1sin2x.

Nếu y=cotu và u=u(x) thì (cotx)′=–u′sin2u.

Công thức đạo hàm cấp 2

Khái niệm công thức đạo hàm cấp hai

Hàm số y=f(x) có đạo hàm tại x∈(a;b).

Lúc đó y’=f'(x) nắm rõ ràng một hàm sô trên (a;b).

Nếu như hàm số y’=f'(x) có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y=f(x) tại x.

Kí hiệu: y” hoặc f”(x).

Ý nghĩa 

a)Ý nghĩa hình học:

• f′(x0) là hệ số góc tiếp tuyến của đồ thị hàm số y=f(x) tại M(x0;f(x0)).
• Khi đó phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại M(x0;f(x0)) là: y–y0=f′(x0).(x–x0)

b)Ý nghĩa vật lí:

• Vận tốc tại thời điểm đó của chuyển động thẳng nắm rõ ràng bởi phương trình s=s(t) tại thời điểm t0 là v(t0)=s′(t0).
• Cường độ tức thời của điện lượng Q=Q(t) tại thời điểm t0 là I(t0)=Q′(t0)

Hàm số y = f(x) có đạo hàm tại x ∈ (a; b).

Khi đó y’ = f'(x) nắm rõ ràng một hàm sô trên (a;b).

Nếu hàm số y’ = f'(x) có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y = f(x) tại x.

Kí hiệu: y” hoặc f”(x).

Ý nghĩa cơ học:

Đạo hàm cấp hai f”(t) là gia tốc tại thời điểm đó của chuyển động S = f(t) tại thời điểm t.

Đạo hàm cấp cao

Cho hàm số y = f(x) có đạo hàm cấp n-1 kí hiệu f ^(n-1) (x) (n ∈ N, n ≥ 4).

Nếu như f ^(n-1) (x) có đạo hàm thì đạo hàm của nó còn được nhắc đên là đạo hàm câp n của y = f(x), y ⁽ⁿ⁾ hoặc f ⁽ⁿ⁾ (x).

f ⁽ⁿ⁾ (x) = [f ^(n-1) (x)]’

Công thức đạo hàm cấp cao:

(x ^m)⁽ⁿ⁾ = m(m – 1)(m – 2)…(m – n + 1).x^{m – n} (nếu m ≥ n)

(x ^m)⁽ⁿ⁾ = 0 (nếu m ≤ n)

Bảng đạo hàm của các hàm số sơ cấp căn bản

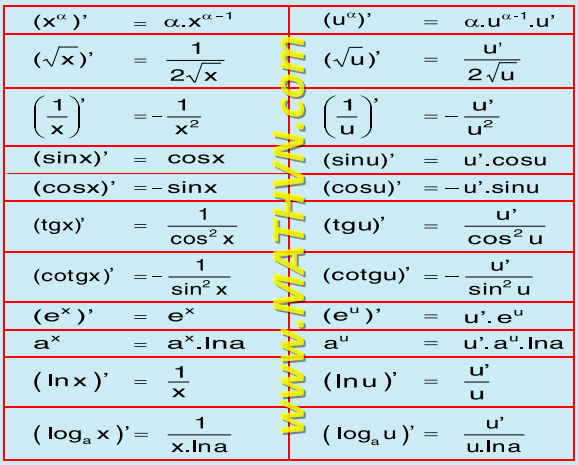
Bảng đạo hàm thường gặp

Các dạng bài tập đạo hàm

Dạng 1: Tính đạo hàm bằng định nghĩa:

Phương pháp: Nếu như tính đạo hàm của hàm số y=f(x) tại điểm x0 bằng khái niệm ta thực hiện các bước:

• Bước 1: Giả sử Δx là số gia của đối số tại x0. Tính Δy=f(x0+Δx)–f(x0).
• Bước 2: Tính limΔx→0ΔyΔx.
• Bước 3: Kết luận.

Ví dụ: Dùng khái niệm hãy tính đạo hàm của hàm số sau: f(x)=x2–3x

Giải:

– Giả sử Δx là số gia của đối số tại x.

Khi đó:

Δy=f(Δx+x)–f(x)=(Δx+x)2–3Δx–3x–x2+3x=(Δx)2+2xΔx=Δx(Δx+2x)

– Tính:

limΔx→0ΔyΔx=limΔx→0Δx(Δx+2x)Δx=limΔx→0(Δx+2x)=2x

– Vậy: f′(x)=2x

Dạng 2: Tính đạo hàm bằng phép toán

Ví dụ:

y=2x+11–3x

⇒y′=(2x+1),(1–3x)–(2x+1)(1–3x),(1–3x)2=2(1–3x)+3(2x+1)(1–3x)2=5(1–3x)2

Dạng 3: Tính đạo hàm hàm hợp

Chú ý: Sau các hàm không phải x thì ta dùng hàm hợp u. Để khỏi quên thì các em có thể trải nghiệm tất cả các bài toán đều cho hàm hợp u vẫn được.

Ví dụ:

y=(x2+x)4⇒y′=4(x2+x)3.(x2+x),=4(2x+1)(x2+x)3

Dạng 4: Tính đạo hàm cấp cao

Phương pháp:

1.Để tính đạo hàm cấp 2,3,4,…ta dung công thức: y(n)=(yn–1)/.

2.Để tính đạo hàm cấp n:

• Tính đạo hàm cấp 1,2,3,… từ đấy suy ra đạo hàm cấp n.
• Dùng phương pháp quy nạp toán học nêu chứng minh công thức đúng.

Ví dụ: Tính đạo hàm cấp n của hàm số: y=1x.

Giải

Ta có:f′(x)=–1×2

f”(x)=1.2×3

f”′(x)=1.2.3×4

….

f(n)(x)=(–1)nn!xn+1

Suy ra: (1x)(n)=(–1)n.n!xn+1

Thật vậy: Khi n=1: Ta có: (1x)‘=(–1).1!x2=–1×2.

Vậy: Mệnh đề đúng khi n=1.

– Khi n=k>1, tức là (1x)(k)=(–1)k.k!xk+1.

Ta cần chứng minh: n=k+1, tức là (1x)(k)+1=(–1)k+1.(k+1)!xk+2

(1x)(k+1)=[(1x)k],=[(–1)k.k!xk+1],=(–1)k.k![1xk+1],=(–1)k+1.(k+1)!xk+2

Vậy: Mệnh đề đúng khi n=k+1.

Kết luận

Trên đây là “12 công thức đạo hàm thường gặp trong đề thi 2021” do Top Uni biên soạn giúp các bạn học sinh chắt lọc được kiến thức cần ghi nhớ khi làm bài về đạo hàm. Nếu thấy bài viết hay và hữu ích, đừng quên để lại bình luận, chia sẻ và like cho tụi mình biết nhé !