Có rất nhiều loại tam giác và tương ứng với mỗi loại tam giác lại có nhiều cách tính diện tích và công thức tính tam giác khách nhau. Ở bài viết này, Top Uni sẽ giới thiệu đến bạn “Tổng hợp các cách tính diện tích tam giác kèm bài tập chi tiết” để bạn có thể dễ dàng áp dụng trong bài thi của mình.
Hình tam giác là gì?
Tam giác hay hình tam giác là một loại hình căn bản trong hình học: hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh với nhau. Tam giác là đa giác có số cạnh ít nhất (3 cạnh). Tam giác bao giờ cũng là một đa giác đơn và luôn là một đa giác lồi (các góc trong luôn nhỏ hơn 180o).
Các kiểu tam giác
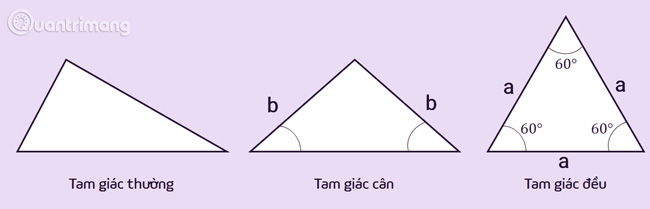
Tam giác thường
Là tam giác dễ dàng nhất, có độ dài các cạnh không giống nhau, số đo góc trong cũng khác nhau. Tam giác thường cũng có khả năng gồm có các trường hợp đặc biệt của tam giác.
Tam giác cân
Là tam giác có hai cạnh bằng nhau, hai cạnh này còn được gọi là hai cạnh bên. Đỉnh của một tam giác cân là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh còn được gọi là góc ở đỉnh, hai góc còn lại gọi là góc ở đáy. Phẩm chất của tam giác cân là hai góc ở đáy thì bằng nhau.
Tam giác đều
Là hoàn cảnh đáng chú ý của tam giác cân có cả ba cạnh bằng nhau. phẩm chất của tam giác đều là có 3 góc bằng nhau và bằng 60
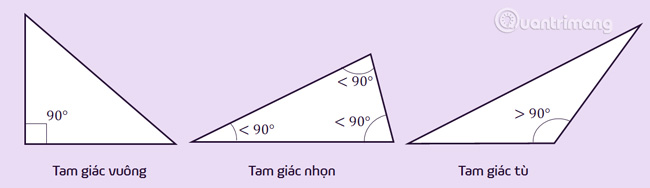
Tam giác vuông
Là tam giác có một góc bằng 90
Tam giác tù
Là tam giác có một góc trong lớn hơn lớn hơn 90
Tam giác nhọn
Là tam giác có ba góc trong đều nhỏ hơn 90toàn bộ góc ngoài lớn hơn 90
Tam giác vuông cân
Vừa là tam giác vuông, vừa là tam giác cân.
Tính diện tích tam giác thường
Tam giác ABC có ba cạnh a, b, c, ha là đường cao từ đỉnh A như hình vẽ:
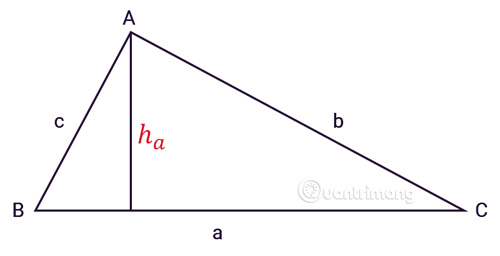
Công thức chung
Diện tích tam giác bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó.
Ví dụ:
Tính diện tích hình tam giác có độ dài đáy là 5m và chiều cao là 24dm.
Giải: Chiều cao 24dm = 2,4m
Diện tích tam giác là
Tính diện tích tam giác khi biết một góc
Diện tích tam giác bằng ½ tích hai cạnh kề với sin của góc hợp bởi hai cạnh đó trong tam giác.
Ví dụ:
Tam giác ABC có cạnh BC = 7, cạnh AB = 5, góc B bằng 60 độ. Tính diện tích tam giác ABC?
Giải:
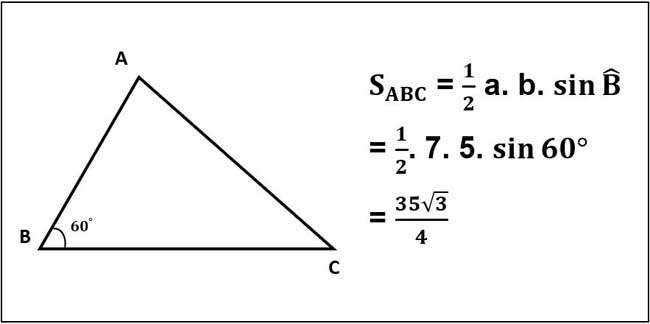
Tính diện tích tam giác khi biết 3 cạnh bằng công thức Heron
Sử dụng công thức Heron đã được chứng minh:
Với p là nửa chu vi tam giác:
Có thể viết lại bằng công thức:
Ví dụ:
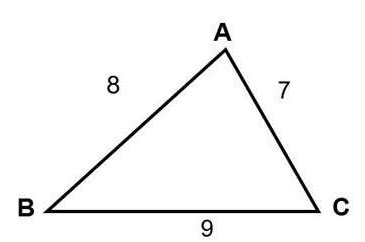
Tính diện tích hình tam giác có độ dài cạnh AB = 8, AC = 7, CB = 9
Giải:
| Nửa chu vi tam giác ABC là
Sử dụng công thức hero ta có |
 |
Tính diện tích bằng bán kính đường tròn ngoại tiếp tam giác (R)
Cách khác: |
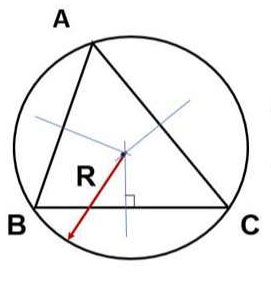 |
Lưu ý: Cần phải chứng minh được R là bán kính đường tròn ngoại tiếp tam giác.
Ví dụ:
Cho tam giác ABC, độ dài các cạnh a = 6, b = 7, c = 5, R = 3 (R là bán kính đường tròn ngoại tiếp tam giác ABC). Tính diện tích của tam giác ABC.
Giải:
Công thức tính diện tích tam giác vuông
– Diễn giải: Công thức tính diện tích tam giác vuông tương tự với cách tính diện tích tam giác thường, đó là bằng1/2 tích của chiều cao với chiều dài đáy. Mặc dù vậy hình tam giác vuông sẽ khác biệt hơn đối với tam giác thường do thể hiện rõ chiều cao và chiều dài cạnh đáy, và bạn không cần vẽ thêm để tính chiều cao tam giác.
Công thức tính diện tích tam giác vuông
S = (A X H) / 2
Diễn giải
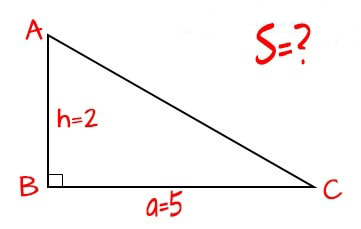
+ Công thức tính diện tích tam giác vuông tương tự với cách tính diện tích tam giác thường, đó là bằng1/2 tích của chiều cao với chiều dài đáy. Vì tam giác vuông là tam giác có hai cạnh góc vuông nên chiều cao của tam giác sẽ ứng với một cạnh góc vuông và chiều dài đáy ứng với cạnh góc vuông còn lại
Công thức tính diện tích tam giác vuông
S = (a x b)/ 2
Trong đó a, b: độ dài hai cạnh góc vuông
Công thức suy ra:
a = (S x 2) : b hoặc b = (S x 2) : a
Bài tập ví dụ
Tính diện tích của tam giác vuông có:
a, Hai cạnh góc vuông lần lượt là 3cm và 4cm
b, Hai cạnh góc vuông lần lượt là 6m và 8m
Lời giải:
a, Diện tích của hình tam giác là:
(3 x 4) : 2 = 6 (cm2)
Đáp số: 6cm2
Diện tích của hình tam giác là:
(6 x 8) : 2 = 24 (m2)
Đáp số: 24m2
Tương tự nếu dữ liệu hỏi ngược về cách tính độ dài, các bạn có thể trải nghiệm công thức suy ra ở trên.
Công thức tính diện tích tam giác cân
Diễn giải:
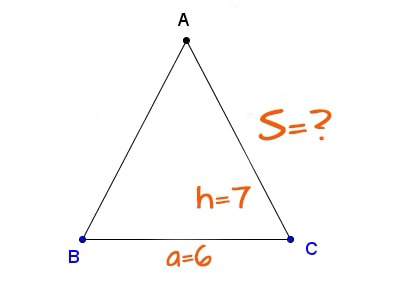
Tam giác cân là tam giác trong đó có hai cạnh bên và hai góc bằng nhau. Trong đó cách tính diện tích tam giác cân cũng tương tự cách tính tam giác thường, chỉ cần bạn biết chiều cao tam giác và cạnh đáy.
Diện tích tam giác cân bằng Tích của chiều cao nối từ đỉnh tam giác đấy tới cạnh đáy tam giác, sau đấy chia cho 2.
Công thức tính diện tích tam giác cân
S = (a x h)/ 2
+ a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)
+ h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
Bài tập
* Tính diện tích của tam giác cân có:
a, Độ dài cạnh đáy bằng 6cm và đường cao bằng 7cm
b, Độ dài cạnh đáy bằng 5m và đường cao bằng 3,2m
Lời giải:
a, Diện tích của hình tam giác là:
(6 x 7) : 2 = 21 (cm2)
Đáp số: 21cm2
b, Diện tích của hình tam giác là:
(5 x 3,2) : 2 = 8 (m2)
Đáp số: 8m2
Bí quyết tính diện tích tam giác đều
Diễn giải:
Tam giác đều là tam giác có 3 cạnh bằng nhau. Trong số đó cách tính diện tích tam giác đều cũng tương tự cách tính tam giác thường, chỉ cần bạn biết chiều cao tam giác và cạnh đáy.
+ Diện tích tam giác cân bằng Tích của chiều cao nối từ đỉnh tam giác đấy tới cạnh đáy tam giác, sau đấy chia cho 2.
Công thức tính diện tích tam giác đều
S = (a x h)/ 2
+ a: Chiều dài đáy tam giác đều (đáy là một trong 3 cạnh của tam giác)
+ h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
Bài tập
* Tính diện tích của tam giác đều có:
a, Độ dài một cạnh tam giác bằng 6cm và đường cao bằng 10cm
b, Độ dài một cạnh tam giác bằng 4cm và đường cao bằng 5cm
Lời giải
a, Diện tích hình tam giác là:
(6 x 10) : 2 = 30 (cm2)
Đáp số: 30cm2
b, Diện tích hình tam giác là:
(4 x 5) : 2 = 10 (cm2)
Đáp số: 10cm2
Dù dùng công thức tính diện tích tam giác nào đi chăng nữa thì các bạn, các em học sinh, sinh viên cần hiểu rằng, không phải lúc chiều cao cũng nằm trong tam giác, lúc này cần vẽ thêm một chiều cao và cạnh đáy bổ sung. Và cần thiết khi tính diện tích tam giác, cần chú ý chiều cao phải ứng với cạnh đáy địa điểm nó chiếu xuống.
Công thức tính diện tích tam giác nâng cao
Ngoài những cách tính diện tích tam giác ở trên, thực tế, toán học còn phổ biến các cách tính diện tích tam giác bằng công thức Heron, tính diện tích tam giác bằng góc và hàm lượng giác. Cụ thể:
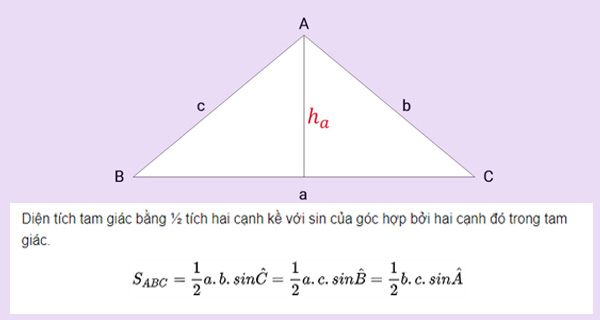
Công thức 1:
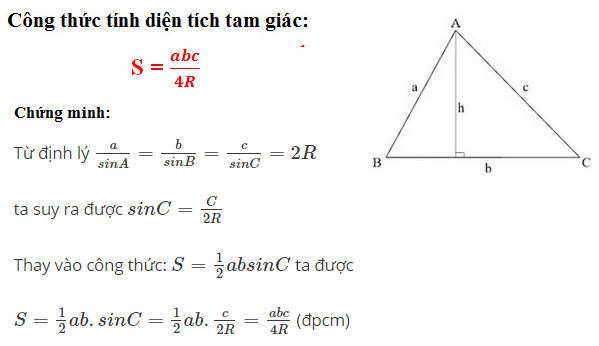
Trong đó:
– a, b, c: Độ dài cạnh của tam giác
– R: Bán kính đường tròn ngoại tiếp tam giác
Công thức 2:
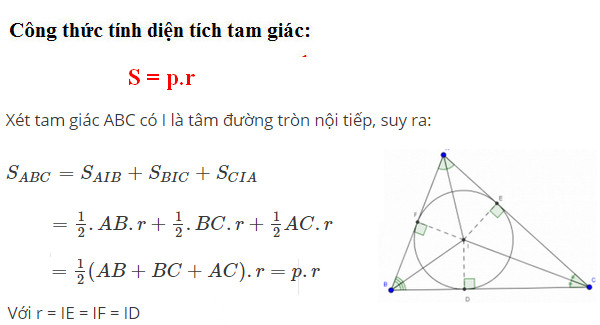
Trong đó:
– p: nửa chu vi tam giác
– r: bán kính đường tròn nội tiếp tam giác
Kết luận
Trên đây là các công thức tính diện tích tam giác chi tiết và ví dụ bài tập cho từng trường hợp để bạn có cái nhìn tổng quan nhất khi tính diện tích tam giác. Nếu thấy bài viết “Tổng hợp các công thức tính diện tích tam giác kèm bài tập chi tiết” do Top Uni tổng hợp hữu ích với bạn, đừng quên để lại bình luận cho tụi mình biết nhé.









